Cálculos de Sistemas Hidráulicos
Aprenda os principais cálculos e fórmulas utilizadas na seleção dos componentes hidráulicos
Por Gustavo Marinho, CFPHS | 23 de Agosto de 2020
Durante o desenvolvimento do projeto de um equipamento hidráulico uma etapa muito importante é a “Seleção e Dimensionamento dos Componentes”. Embora existam muitas maneiras diferentes de se obter os mesmos resultados no que se diz respeito aos cálculos de dimensionamentos de componentes de circuito hidráulicos, este artigo tem por objetivo estressar e detalhar um pouco mais a fundo as formulas e cálculos mais comumente utilizados por engenheiros e projetistas de sistemas hidráulicos e pneumáticos.
Na figura abaixo podemos ver uma imagem detalhando um fluxograma que entendo ser a sistemática de passo-a-passo mais praticada por especialistas em design.
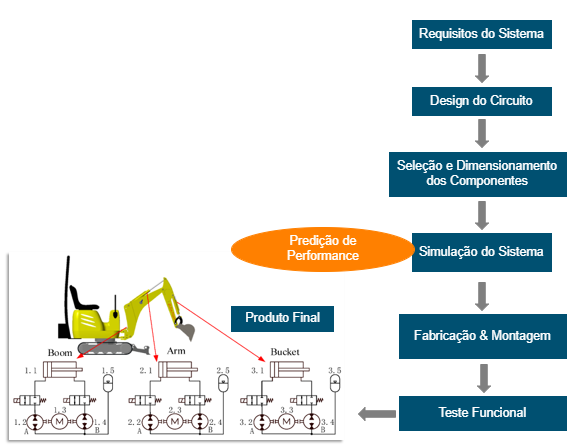
Sumário
Embora as fórmulas de sistemas hidráulicos e pneumáticos sejam ferramentas úteis para especificar os componentes e recursos do sistema; outros fatores como eficiências mecânicas, dinâmica de fluidos e limitações de material também devem ser considerados.
Mesmo tendo tomado bastante cuidado para verificar se as conversões e cálculos deste artigo estão corretos, não tenho como objetivo aqui assumir nenhuma garantia, ou responsabilidade legal ou responsabilidade pela exatidão, integridade ou utilidade de qualquer das informações fornecidas neste artigo. Dito isto, vamos analisar alguns dos cálculos mais uteis para dimensionamento de componentes e sistemas.

Cálculos Hidráulicos de Bombas
Potência necessária para o correto funcionamento de uma bomba:
GPM (Gallons per Minute) x PSI (Pound Square Inch) x 0,0007 (este é um cálculo de ‘regra de geral’)
Exemplo: Quantos HPs (cavalo-vapor) são necessários para acionar uma bomba de 5 GPM a 1.500 PSI?
GPM = 5 PSI = 1500
GPM x PSI x 0,0007 = 5 x 1500 x 0,0007 = 5,25 (HP) cavalo-vapor
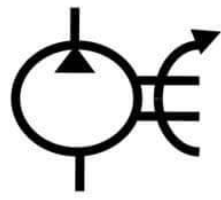
Deslocamento da bomba necessário para o fluxo de saída em GPM:
231 x GPM ÷ RPM (Revolutions Per Minute)
Exemplo: Qual deslocamento é necessário de uma bomba para produzir 5 GPM a 1.500 RPM?
GPM = 5
RPM = 1500
231 x GPM ÷ RPM = 231 x 5 ÷ 1500 = 0,77 pol³ por revolução (ciclo)
Fluxo de saída da bomba (em galões por minuto):
RPM x deslocamento da bomba ÷ 231
Exemplo: Quanto óleo será produzido por uma bomba de 2,5 polegadas cúbicas operando a 1200 RPM?
RPM = 1200
Deslocamento da bomba = 2,5 pol³ (polegadas cúbicas)
RPM x Deslocamento da bomba ÷ 231 = 1200 x 2,5 ÷ 231 = 12,99 GPM

Cálculos Hidráulicos de Cilindros
Área da extremidade da haste do cilindro em pol2 (polegadas quadradas):
Área da extremidade cega – área da haste
Exemplo: Qual é a área da extremidade da haste de um cilindro de 6 pol de diâmetro que possui uma haste de 3 pol de diâmetro?
NOTA: Para facilitação o símbolo ” será utilizado como abreviação de polegadas.
Área da extremidade cega do cilindro = 28,26 pol2
Diâmetro da haste = 3 “
O raio é 1/2 do diâmetro da haste = 1,5 “
Raio2 = 1,5 “x 1,5” = 2,25 “
π x Raio 2 = 3,14 x 2,25 = 7,07 pol2
Área da extremidade cega – Área da haste = 28,26 – 7,07 = 21,19 pol2
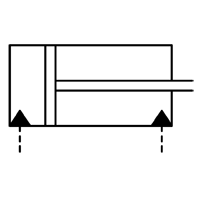
Área da extremidade cega do cilindro (em polegadas quadradas):
PI x (raio do cilindro) 2
Exemplo: Qual é a área de um cilindro de 6 “de diâmetro?
Diâmetro = 6 “
O raio é 1/2 do diâmetro = 3 “
Raio2 = 3 “x 3” = 9 “
π x (raio do cilindro) 2 = 3,14 x (3) 2 = 3,14 x 9 = 28,26 pol2
Saída de vazão da extremidade cega do cilindro (GPM):
Área da extremidade cega ÷ Área da extremidade da haste x GPM entrada
Exemplo: Quantos GPM saem da extremidade cega de um cilindro de 6 “de diâmetro com uma haste de 3” de diâmetro quando temos 15 galões por minuto colocados na extremidade da haste?
Área da extremidade cega do cilindro = 28,26 pol2
Área da extremidade da haste do cilindro = 21,19 pol2
Entrada GPM = 15 GPM
Área da extremidade cega ÷ Área da extremidade da haste x GPM entrada = 28,26 ÷ 21,19 x 15 = 20 GPM
Força de saída do cilindro (em libras):
Pressão (em PSI) x Área do Cilindro
Exemplo 1: Qual é a força de “empurrar” de um cilindro de 6 “de diâmetro operando a 2.500 PSI?
Área da extremidade cega do cilindro = 28,26 pol2
Pressão = 2.500 psi
Pressão x área do cilindro = 2.500 X 28,26 = 70.650 libras
Exemplo 2: Qual é a força de tração de um cilindro de 6 “de diâmetro com uma haste de 3” operando a 2.500 PSI?
Área da extremidade da haste do cilindro = 21,19 pol2
Pressão = 2.500 psi
Pressão x área do cilindro = 2.500 x 21,19 = 52.975 libras

Velocidade do cilindro (em polegadas por segundo):
(231 x GPM) ÷ (60 x área líquida do cilindro)
Exemplo: Quão rápido um cilindro de 6 “de diâmetro com uma haste de 3” de diâmetro se estenderá com 15 GPM de entrada?
GPM = 6
Área líquida do cilindro= 28,26 pol2
(231 x GPM) ÷ (60 x Área líquida do cilindro) = (231 x 15) ÷ (60 x 28,26) = 2,04 polegadas por segundo (pol/s)
Quão rápido ele se retrairá?
Área do cilindro líquido = 21,19 pol2
(231 x GPM) ÷ (60 x Área líquida do cilindro) = (231 x 15) ÷ (60 x 21,19) = 2,73 polegadas por segundo
GPM de fluxo necessário para a velocidade do cilindro:
Área do cilindro x comprimento do curso em polegadas ÷ 231 x 60 ÷ Tempo em segundos para um ciclo
Exemplo 1: Quantos GPM são necessários para estender um cilindro de 6 “de diâmetro em 8 polegadas em 10 segundos?
Área do cilindro = 28,26 polegadas quadradas
Comprimento do curso = 8 polegadas
Tempo para 1 curso = 10 segundos
Área x Comprimento ÷ 231 x 60 ÷ Tempo = 28,26 x 8 ÷ 231 x 60 ÷ 10 = 5,88 GPM
Exemplo 2: Se o cilindro tiver uma haste de 3″ de diâmetro, quantos GPM são necessários para retrair 8 polegadas em 10 segundos?
Área do cilindro = 21,19 polegadas quadradas
Comprimento do curso = 8 polegadas
Tempo para 1 curso = 10 segundos
Área x Comprimento ÷ 231 x 60 ÷ Tempo = 21,19 x 8 ÷ 231 x 60 ÷ 10 = 4,40 GPM
Pressão de fluido em PSI necessária para elevar uma carga (em PSI):
Libras de força necessárias ÷ Área do cilindro
Exemplo 1: Que pressão é necessária para desenvolver 50.000 libras de força de “empurrar” de um cilindro de 6 “de diâmetro?
Libras da Força = 50.000 libras
Área da extremidade cega do cilindro = 28,26 pol2
Libras de força necessárias ÷ Área do cilindro = 50.000 ÷ 28,26 = 1.769,29 PSI
Exemplo 2: Qual pressão é necessária para desenvolver 50.000 libras de força de tração de um cilindro de 6 “de diâmetro que tem 3” de diâmetro da haste?
Libras da Força = 50.000 libras
Área da extremidade da haste do cilindro = 21,19 polegadas quadradas
Libras de força necessárias ÷ Área do cilindro = 50.000 ÷ 21,19 = 2.359,60 PSI

Cálculos Hidráulicos de Motores
GPM de fluxo necessário para a velocidade do motor do sistema:
Deslocamento do motor x RPM do motor ÷ 231
Exemplo: Quantos GPM são necessários para acionar um motor de 3,75 polegadas cúbicas a 1.500 rpm?
Deslocamento do motor = 3,75 polegadas cúbicas por revolução
RPM do motor = 1500
Deslocamento do motor x RPM do motor ÷ 231 = 3,75 x 1500 ÷ 231 = 24,35 GPM
Velocidade do motor do sistema com um GPM de entrada:
231 x GPM ÷ Deslocamento do motor de fluido
Exemplo: Quão rápido um motor de 0,75 polegada cúbica girará com entrada de 6 GPM?
GPM = 6
Deslocamento do motor = 0,75 polegadas cúbicas por revolução
231 x GPM ÷ Deslocamento do motor de fluido = 231 x 6 ÷ 0,75 = 1.848 RPM
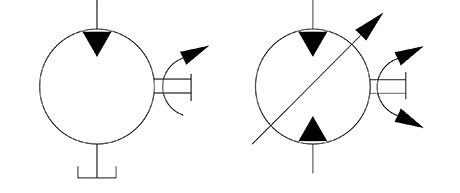
Torque do motor com determinado valor de pressão e deslocamento:
PSI x Deslocamento do motor ÷ (2 x π)
Exemplo: Quanto torque um motor de 2,5 polegadas cúbicas desenvolve a 2.000 psi?
Pressão = 2.000 psi
Deslocamento do motor = 2,5 polegadas cúbicas por revolução
PSI x deslocamento do motor (2 x π) = 2.000 x 2,5 ÷ 6,28 = 796,19 polegadas libras
Torque do motor com um determinado valor de GPM, PSI e RPM:
GPM x PSI x 36,77 ÷ RPM
Exemplo: Quanto torque um motor desenvolve a 1.200 psi, 1.500 rpm, com entrada de 10 gpm?
GPM = 10
PSI = 1.500
RPM = 1200
GPM x PSI x 36,7 ÷ RPM = 10 x 1.500 x 36,7 ÷ 1200 = 458,75 polegadas libras por segundo

Torque do motor com um determinado valor de potência e RPM:
Potência x 63025 ÷ RPM
Exemplo: Quanto torque é desenvolvido por um motor a 12 cavalos e 1750 rpm?
Horsepower = 12
RPM = 1750
Potência x 63025 ÷ RPM = 12 x 63025 ÷ 1750 = 432,17 polegadas libra.

Cálculos de Fluidos e Tubulação
Velocidade do fluido através da tubulação:
0,3208 x GPM ÷ Área interna
Exemplo: Qual é a velocidade de 10 GPM passando por uma tubulação de 1/2″ de diâmetro?
GPM = 10
Área interna = 0,304 (veja a nota abaixo)
0,3208 x GPM ÷ Área interna = 0,3208 x 10 ÷ 0,304 = 10,55 pés por segundo (pés/s ou ft/s)
NOTA: O diâmetro externo do tubo permanece o mesmo, independentemente da espessura do tubo. Um tubo para sistemas de ata pressão tem uma parede mais espessa do que um tubo de sistema padrão, então o diâmetro interno do tubo de um sistema de alta pressão é menor do que o diâmetro interno de um tubo de sistema padrão. A espessura da parede e o diâmetro interno dos tubos podem ser encontrados em gráficos prontamente disponíveis.
Tubos de aço para sistemas hidráulicos também mantém o mesmo diâmetro externo, independentemente da espessura da parede.
Os tamanhos das mangueiras indicam o diâmetro interno das mesmas. Uma mangueira de 1/2 “de diâmetro tem um diâmetro interno de 0,50 polegadas, independentemente da classificação de pressão da mangueira.

Tamanhos de tubulação sugeridos:
– As linhas de sucção da bomba devem ser dimensionadas de forma que a velocidade do fluido fique entre 2 e 4 pés por segundo.
– As linhas de retorno de óleo devem ser dimensionadas de forma que a velocidade do fluido fique entre 10 e 15 pés por segundo.
– As linhas de suprimento de pressão média devem ser dimensionadas de forma que a velocidade do fluido fique entre 15 e 20 pés por segundo.
– As linhas de suprimento de alta pressão devem ser dimensionadas de forma que a velocidade do fluido seja inferior a 30 pés por segundo.
Um gráfico muito útil para a analise de dimensionamento de tubulações de sistemas hidráulicos é o Nomograma (ou Nomograph) que pode ser visto abaixo:
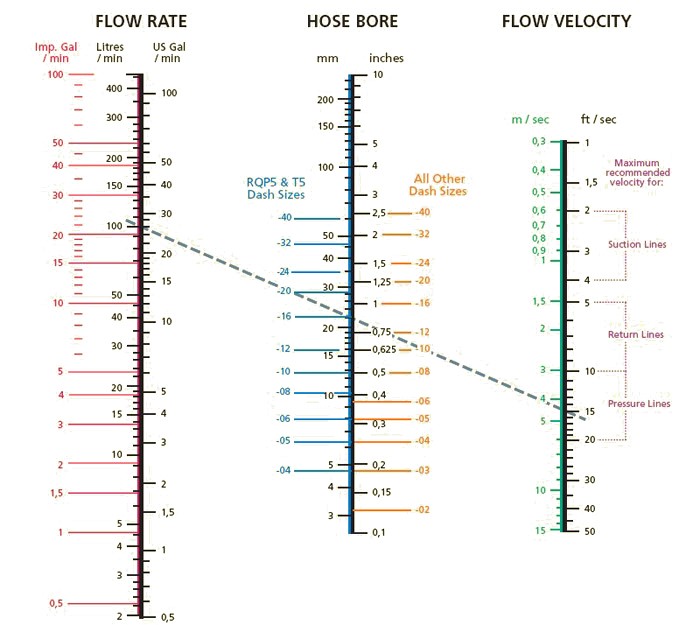
Referências:
Hydraulic Specialist Study Manual (IFPS)
https://hidraulicaepneumatica.com/engineering-toolbox/







Este post tem 3 comentários
Espetacular! Excelente trabalho.
muito bom material,muito proveitoso expricação muito boa,Parabém
Excelente , continue !!!